Qu'est-ce que la capacitance ?
La transmission d’un signal électrique à travers un câble est sujette à des lois physiques universelles.
Ce qui est valable pour une ligne électrique haute-tension l’est autant pour une modulation audio ou un signal numérique (transmis en impulsions électriques). Plus la modulation électrique traversant un conducteur est faible, plus ces contraintes ont d’incidences sur l’intégrité du message. Celui-ci peut être altéré par des forces résistantes internes ou externes.
On parle de “conductivité”, “résistance”, “impédance”, “réactance”, “inductance”, “capacité”, “capacitance” : qu’en est-il de ces termes alambiqués ?
Avant tout, précisons que pour protéger une si faible modulation sur de grandes longueurs (dans des câbles que l’on souhaite souples et ergonomiques) on porte ces signaux sur des brins, certes isolés individuellement, mais également torsadés entre eux. Afin que chaque brin soit le moins exposé à des perturbations électromagnétiques dans un axe donné .
Cette configuration en spirales (que l’on retrouve dans les câbles réseaux, DMX, microphones, Haut-Parleurs, multicoaxiaux...) crée une bobine à induction. La différence de potentiel de tension entre les brins va accumuler une charge entre les conducteurs, minime mais contraignante.
• La conductivité électrique est la propriété d'un matériau à conduire un courant électrique.
Elle s’exprime en Siemens par mètre. Plus elle est élevée, plus le courant passe avec facilité.
• Inversement, au passage du courant se dresse une force résistive exprimée en Ohms :
Dans un courant continu c’est la résistance électrique, force proportionnellement opposée à la conductivité de ce même matériau. Plus la résistance est faible, meilleure est la conductivité. U=R.I ou R = U/I
L’impédance est son équivalent dans un courant alternatif sinusoïdal, ce qui est le cas dans la modulation audio ou dans la transmission d’un flux numérique.
Pour être plus précis, l'impédance aux bornes d’un circuit ou d’un composant est un nombre complexe (il faut réviser ses cours de lycée) défini par un module — qui correspond à la résistance : rapport tension/courant (I Z I = Vo/Io) — et par un argument — φ = φv - φi, qui manifeste le déphasage qui se forme par rapport au signal d’origine —
Il est donc essentiel de tenir compte de l’impédance globale d’un montage, harmoniser l’ensemble des impédances pour minimiser les pertes.
L’impédance peut également être présentée sous sa forme partie réelle résistive (R) + partie imaginaire réactive, qu’on appelle réactance ( X ) : Z = R + jX.
1. Si la réactance X = 0, l’impédance est purement résistive : Z = R, comme dans un courant continu.
Toutefois, si elle est inférieure ou supérieure à 0 elle est l’expression du champ magnétique créé par le courant.
2. Supérieure elle est inductive, on parlera alors d’inductance. XL = 2πfL avec L coefficient d’induction en Henry. On retrouve notamment ce cas de figure dans la structure d’un transformateur électrique ou de selfs bobinage...
3. Inférieure, elle est qualifiée de capacitive : c’est la capacitance. Même s’il est usuel de la définir comme XC = 1 / 2πfC avec C la Capacité en Farad, cette capacitance est en fait obligatoirement négative. On pourrait considérer lui ajouter un “–” en amont mais nous allons voir qu’elle se soustrait à l’inductance dans le calcul global. Appliquer ce marqueur négatif à ce stade fausserait la logique qui suit.
On voit dans ces deux derniers cas que la réactance est tributaire de la fréquence et manifeste un déphasage entre la tension et le courant, d’autant plus fragrant que la fréquence est grande.
Ainsi sur une modulation audio, si la réactance est trop importante (qu’elle soit inductive ou capacitive) le son sera altéré signicativement sur les fréquences aiguës et de façon dégressive vers les fréquences basses.
Donnant nature à un son étouffé sinon à des interférences liées au retard de transmission des fréquences affectées. Sur un signal numérique, les ondes carrées risquent d’être altérées en dent de scie rendant le signal incompréhensible.
Tout le monde n’est pas familier avec le principe de nombres complexes ou d’imaginaire en mathématique, on peut également considérer les forces impliquées dans l’impédance sous leur forme vectorielle : c’est le principe du diagramme de Fresnel.
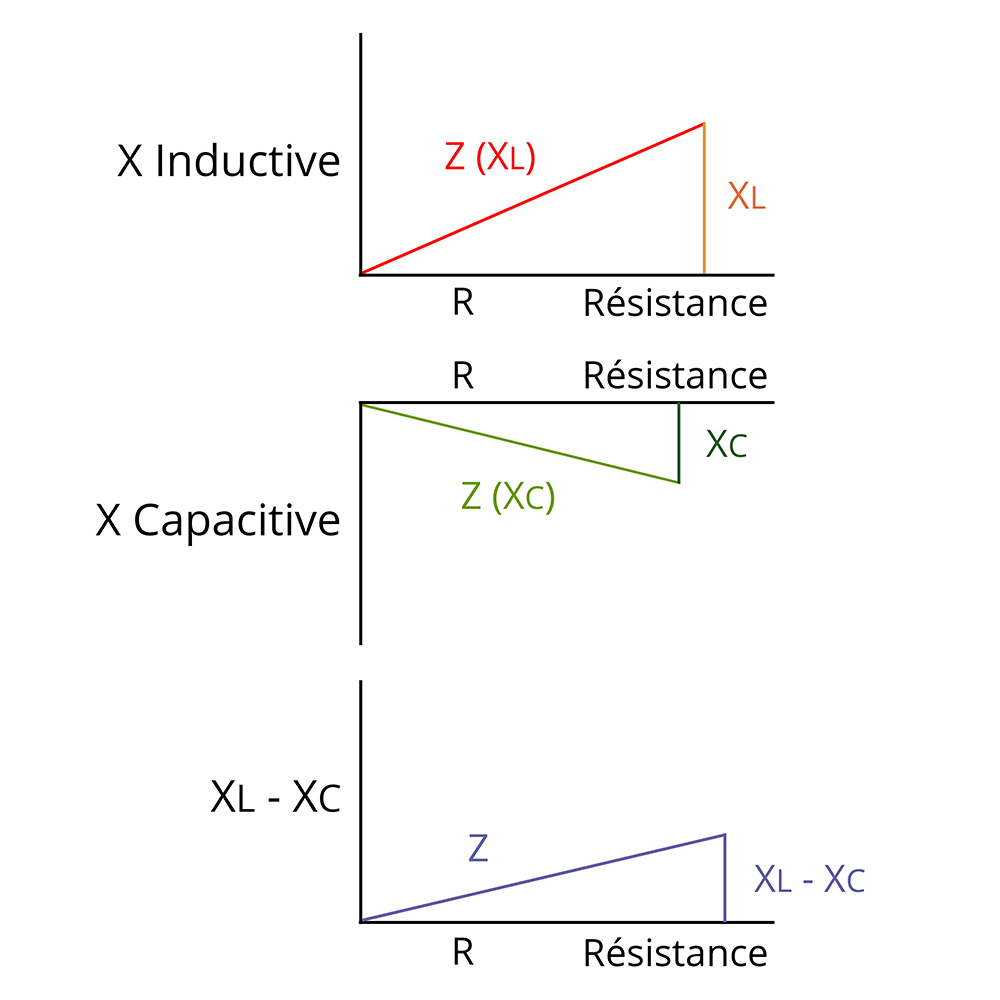
Dans le tableau ci-dessus, nous trouvons en abscisse la résistance physique. En ordonnée, la réactance : positive (XI, Inductance) et négative (XC, Capacitance)
→ → →
𝑍 = 𝑅 + (𝑋𝐿 − 𝑋𝐶)
• On arrive alors à cette formule Z2= R2 + (XL – XC)2 (oui oui ! Le Théorème de Pythagore ! Nous avons des triangles rectangles dont nous cherchons l'hypoténuse et dont nous avons les autres valeurs des côtés).
Plus la capacité est faible, plus la capacitance est forte. Donc plus le rapport (XL – XC) est faible... soit, au vu de la dernière formule évoquée : l’impédance proche d’une simple force résistive, Z = R, sans déphasage.
Voilà pourquoi les fabricants de câbles donnent fréquemment la valeur de capacité de leur câble, qu’ils souhaitent la plus basse possible. Plus la capacité est faible, meilleures sont les propriétés du câble.
• Capacité :
On parle de capacité dans un système susceptible d'accueillir une charge entre deux pôles : un condensateur, un accu, une bobine... donc également dans notre contexte de brins torsadés. C’est le quotient de la charge portée entre les armatures, définie en Coulombs , par la différence de Tension (Volts) entre celles-ci à l’instant t : C = Q/U.
Elle s’exprime en Farad. Dans le cas d’un câble, au vu des très faibles charges accumulées entre les brins, on la définit en picoFarad par mètre.
On peut réduire cette capacité par la nature de l’isolant, son épaisseur ou en réduisant le diamètre du conducteur mais ces différentes options entraînent d’autres contraintes : habile histoire de compromis.
Images et Textes : la-bs.com®